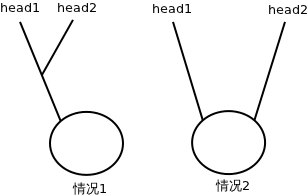
冈和金的约见，是在在世界之树的顶端, 这对奇特的父子，让无数人期待了15年…

概念和起源

LL(*)是由Terrence Parr教授创造的，为使用LL分析的语法解析器做超前查看(look ahead)的一种算法。按照Parr教授的说法，这个算法从最初的想法至今的完善和调整已经历了15年。目前该算法的一个著名的实现在antlr3中。

特点，n言以蔽之…

• 对于语法产生式分支的预测判断，走LL分析路子的解析器，其能力完全取决于能超前查看多少个token。传统地讲，LL(1), LL(2)直至LL(k)，就是在讲该解析器能够在语法分析过程中超前查看1, 2, k…个token。
• 而LL(*)的意思就是，它在语法解析的过程中，超前查看的token个数不是固定的，是可伸缩的，不过这一点LL(k)分析也能做到(在k范围之内…)；
• 但是，LL(*)还能越过一些重复出现的token，“到达”这些重复出现的token之后的token来做分析，这一点LL(k)是无法办到的(LL(k)无法意识到有token在循环出现，不管情况如何，它都将在尝试k个token之后放弃)；
• 如果将超前查看的决策逻辑画成DFA的话，就是这样的一种形式：
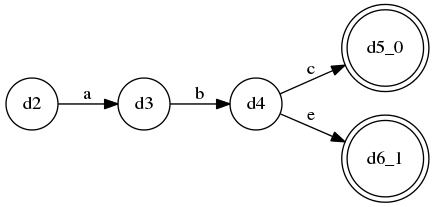
  • 这张图画的是这种语法规则的超前查看决策情况：A ::= a b c | a b e, 显然这是一个LL(3)语法；
  • 但是这样的语法: A ::= a b* c | a b* e是无法被LL(k)识别的，因为中间的b*代表“0个或多个b”(kleene闭包)，这并不是一个固定的重复次数，因此LL(k)无法识别，for any k…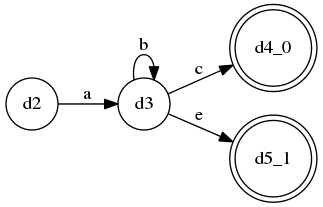
  • 但是，LL(*)算法能够构造出这样的DFA来识别它：
  • 也就是说，传统LL(k)的look ahead DFA是不带环的，而LL(*)算法能构造出带环的DFA来做判断，它能越过无穷多个存在于环上的token，从而“到达”环之后的token继续做判断。
• 上面的A ::= a b* c | a b* e语法使用了“kleene闭包”表示法来表示“0个或多个”，这种表示法在正则表达式中很常见；事实上，基于LL(*)算法实现的语法解析器生成器(比如antlr3)对Kleene闭包表示法特别友好，可以鼓励使用，还能顺便解决一些LL分析法所不允许的“左递归”。
• 大多数情况来讲，LL(*)的识别能力弱于LR(k)，但也有少数情况是LR(k)识别不了但LL(*)可以的，所以LL(*)与LR(k)之间并没有严格的强弱顺序。
• LL(*)本身对语法的识别能力也是有限的，比如它无法区分”具有相同的递归规则前缀”的多个分支，这种情况是要尽量避免的，大多数能够较容易地改写;
• 对于LL(*)不能正确分析的情况，还能引入”Semantic Predicate”(语义断言)来辅助判断, Semantic Predicate可以是任何逻辑，只要返回一个bool值就行；有了Semantic Predicate的辅助，LL(*)甚至能够parse一些上下文相关的语法，实际上它能parse C++

主要算法及其实现(python)

Parr教授在2011年发表的paper”LL(*): The Foundation of the ANTLR Parser Generator”中详细描述了这个算法，下面就是其主要过程，具体的代码实现(python)在工程llstar中

week2主要讲了master method，感觉从来没有听过如此清晰有条理的介绍master method的讲解，不得不佩服Tim Roughgarden教授的功力。
从一些随课笔记总结起来，master method是用来预估divide and conquer算法的大O时间复杂度的公式；它要求divide的时候“所有sub-problems的规模都相等”才能适用。
要使用master method, 首先要将算法的时间消耗函数写成递推公式形式： $$T(n) <= aT(\frac{n}{b}) + O(n^d)$$ 其中T(n)是本层递归所消耗的时间，$T(\frac{n}{b})$自然就是下一层递归所消耗的时间了，b就是每次往“下层”递归调用时问题规模缩小的倍率，a就是代码中递归调用的个数；$O(n^d)$ 是将递归调用之外的其它代码的时间开销写成关于输入规模n的指数形式，d就是这个指数。
基础情况： 当n足够小时，T(n) <= 一个常数
a,b,d与输入规模无关。
那么，根据a,b,d的情况，T(n)可能被表示为三种情况：

一般来讲，如果使用的解析器生成器是基于LL分析法来解析文本的话(比如antlr)，我们就需要在编写语法规则的时候避免左递归。
虽然有一套成熟的、公式化的方法来去除左递归，但它会影响原有文法的结合顺序、优先级，或者多出一些本不需要的、额外的产生式。
例如，有左递归语法规则：

addition ::= addition '+' factor
           | factor

这个式子其实是想要表达一个“一连串+号组成的和”的表达式，例如1+2+3+4；
假设目前的输入就是1+2+3+4, 那么超前查看带来的选择应该是addition '+' factor这个产生式；于是在parser的代码中立刻就又直接调用了addition()方法，但注意，整个递归过程没有消耗掉任何token…也就是说，当流程再次递归到addition函数里时，输入1+2+3+4并没有任何改变，这又会进入下一轮递归…很快就会overflow。
这个问题，除了机械性地按照公式来消除左递归外，还可以改写语法规则，使其成为右递归语法：

addition ::= factor '+' addition
           | factor

这样就不用stackOverFlow了，但是带来另一个问题：这使得我们的’+’加法成为了一个’右结合’的运算…
也就是说，1+2+3+4的计算次序是这样的：1+(2+(3+4))
还好这里是“加法”，整数集合和加法运算构成“阿贝尔群(可交换群)”，满足交换律，所以就算实现成右结合的也能蒙混过关…但减法呢？除法呢？

algo-class还是挺有意思的，一上来就讲merge sort；介绍了分治法以及”piggyback”的思路…当作是复习吧：

分治法(divide and conquer)

1. divide into smaller problems
2. conquer sub-problems recursively
3. combine solutions of problems into one for the original problems

而”piggyback”的意思就是：记住一些经典算法的实现，遇到类似问题的时候，可以将要解决的问题“搭载”到那些经典算法上面，一般都具有和那些经典算法相同的平均时间复杂度；相当于是把那些经典算法当作一个个“模式”或者“骨架”了(所以说平时经常听到的经典算法还是要熟悉熟悉的，很多地方能派上用场)。

这一周围绕merge sort来讲divide and conquer真是再合适不过了；而作业“Count Inversions”就是一个将场景piggyback到merge sort上的一个典型例子； 作业给出了一个包含10W行数据的文本文件，每一行一个随机数字，要求找出这10W个数字中的所有Inversions。我用python实现如下：

def countInversions(arr):
    length = len(arr)
    if length == 0 or length == 1:
    return (0, arr) 
    mid = int(length / 2)
    (leftCount, leftSortedArr) = countInversions(arr[0:mid])
    (rightCount, rightSortedArr) = countInversions(arr[mid:length])
    (mergedCount, mergedSortedArr) = mergeCount(leftSortedArr, rightSortedArr)
    return (leftCount + rightCount + mergedCount, mergedSortedArr)

def mergeCount(lArr, rArr):
    count = 0
    mergedArr = []
    i = 0
    j = 0
    lenl = len(lArr)
    lenr = len(rArr)
    while i < lenl and j < lenr:
    if lArr[i] > rArr[j]:
        count += lenl - i # key line
        mergedArr.append(rArr[j])
        j += 1
    else:
        mergedArr.append(lArr[i])
        i += 1
    if i < lenl:
    mergedArr.extend(lArr[i:lenl])

    if j < lenr:
    mergedArr.extend(rArr[j:lenr])
    return (count, mergedArr)

import sys
if len(sys.argv) < 2:
    print 'usage: python countInversionInAFile path_to_file'
    exit(1)
numbers = [int(line) for line in open(sys.argv[1], 'r')]
print countInversions(numbers)[0]

程序或许想起来简单但实际上要正确还是要费点功夫的；有些地方没想到的还非得debug才能看清楚为什么，比如程序中标注为”key line”那里，本来我写的是count += 1的但怎么都不对，后来debug才看出来应该写count += lenl - i。

另外，本来打算跟2门课程的，但现在看来我这忙碌的程序员完全没有时间…只好放弃“机器人汽车”那门课目前专门跟这一门了，毕竟“算法”的可操作性要强一些…

dropincc.java为了使得用户能够在java语言中直接定义新语言的词法、语法规则，API设计采用了串接与组合(cascading & composition)风格的FluentInterface形式。

这种形式能够使得这一套API看起来更具有“业务语义”，而不需要像antlr等其它工具一样强迫用户去学习全新的另外一种含有业务语义的DSL。
新语言的词法、语法规则被用户直接在java语句里书写、执行，其实得到的是dropincc.java这个CC工具的内部概念的AST。这个AST其实与“让用户学习一套DSL，然后编写，然后编译这些DSL得到的AST”是一样的。
也就是说 —— dropincc.java里面很重要的一个理念就是：像书写字面量一样书写CC工具的AST(AST literal???)。

注意：强调一下这里说的AST并非用户想要实现的新语言的AST，我指的是dropincc.java这个工具其内部表达词法、语法规则的内部形式。

经过一些初步的尝试，我认为在java中定义出这样一套API是完全可行的，其中一些值得列出的、具有代表性的点如下：

做这么个小lib的动机？

其实由于java语言先天缺陷的元编程能力，在java的圈子里很少有人提到“DSL”的概念，就算有也是说说而已。与之相比，一些其它语言ruby, python, lisp等等，得益于其强大的元编程能力，直接利用自身语法特性，取一块语法子集，利用一些对象、类生命周期切入函数或者宏系统两三下就DSL ‘on-the-fly’了，这种便利性可能由java的设计目标来看，恐怕永远也无法达到了。
那么，在java里面想实现一个DSL，恐怕就得走“外部DSL(详见Fowler的文章: DomainSpecificLanguage)”的路子。
而“外部DSL”这条路并不好走，说白了也就是自己做词法、语法、语义分析，自己生成目标语言代码去执行真正的逻辑；也就是做一个编译器前端外加一段解释执行逻辑；编译器前端，虽然业界看上去有很多很多工具可以直接采用，但是这些工具，目前看来，我认为还是太“General purpose”了，它们往往要求使用者学习它们自己规定的一套用作表达词法、语法规则的DSL，然后提供一个特殊的编译程序，用作编译你用它的DSL写的这些词法、语法文件，最终生成你想要的、基本不可读的编译器前端代码 —— 放到你的项目中去使用；
这种形式的工具在目前的编译器前端生成器中占大多数，使用上绝对称不上是“便利”。除了它用作描述规则的DSL需要使用者学习之外，其使用过程涉及好几个步骤与环境，是很麻烦的一件事情。
曾经有一次，一个同学试图使用antlr来做一个类似SQL子集的DSL，他花很多时间与antlr本身的语法文件、IDE “antlrworks”作斗争…频繁地在eclipse, 命令行, antlrWorks之间切换；我就想，做一个这样的DSL，是否真的用得上这么多工具？是否真的用得上号称能parse C++的antlr？这些事情能否全部在一个工作环境内搞定？比如eclipse？ 而来自rsec的启发让我觉得java似乎更应该有这样一个东西：

1. 以java的语法来新增词法、语法规则，不需要学习新的语法；
2. 不需要依赖外部环境，仅在java开发环境中就能完成新语言的定义与编译器前端程序的生成；
3. 虽然java是静态类型编译型语言，但整个新语言构建过程应该看上去是“动态的”、“解释性”的，这样“体验”才会好；
4. 这个库要小、要没有其它三方库依赖，仅依靠JDK自带库就能使用；
5. 在使用过程中尝试推行一些好的实践，确保大多数普通青年不会“自找麻烦”，比如“限制词法规则必须为正规文法(或者说乔姆斯基3型文法)”。

而Dropincc.java正是以上述几点为设计目标的一个小巧(但足够强大)的编译器生成器。

Octopress插件：octopress-tagcloud相当nice，不过在使用的时候，若是blog整体采用了非ascii码的编码格式(比如utf-8)就会出现类似这样的错误：

Liquid error: incompatible encoding regexp match (ascii-8bit regexp with utf-8 string)

其实是由于octopress-tagcloud的插件文件：plugins/tag_cloud.rb文件本身是ascii编码所致:

$ chardet tag_cloud.rb
tag_cloud.rb: ascii (confidence: 1.00)

tag_cloud.rb中很多地方用到了ruby的正则表达式，而ruby的正则表达式在匹配的时候，默认是按照“代码源文件”的编码格式(在这里是ascii)进行匹配的，而若我的blog是utf-8编码的话就会出现上述错误。

解决办法有二：

1. 将tag_cloud.rb转成utf-8…
2. 更改tag_cloud.rb中所有的正则表达式声明，加上u选项(根据这里的说明，u的意思就是以utf-8编码格式来进行匹配)，即，若原正则式是：/regexp/, 则改成：/regexp/u

其实早就看好的，不过一直没仔细上淘宝询问和调查；
现在在网上买电脑其实也还不错的；
她们平时也就拿电脑来偷偷菜，看看电影，玩玩小游戏逛逛taobao，这样的电脑跑到“电脑城”一问，人家跟他说要4k+才能拿下…我说这不坑爹么？行了，网上搞一套吧，拿回来自己装，心理预期价格2k左右 —— 反正不用买显示器。
对于这些“平民级”的PC需求，我好像一直对AMD体系情有独钟，包括我自己的台式也是AMD…话说我对台式机的需求还真是平民中的平民啊，反正我又不玩什么高端的游戏:)

好了， 配置列表:

1. AMD a6-3650, 盒装带风扇，648元(小贵哦，不过看在它4核再加上显示核心的份上还行)
2. 映泰a75 MH，全固态，小板子，主要是拿来配CPU的FM1插口，不管怎么说主板作为最重要的配件可要弄好一点，模拟/数字/HDMI接口都有(445元)
3. 内存威刚 2G DDR3 1333 * 2 (152元, 2根用来组成双通道的，4g他们装个32位win7应该够了吧…)
4. 硬盘WD500G WD5000AAKX 16M蓝盘 SATA3 (539元！好贵啊…最近硬盘水患涨价，不过总不能不要硬盘吧…)
5. 电源航嘉冷钻2.3+, 300w (199元, 这玩意儿只能装进大机箱…)
6. 华硕DVDRW DRW-24D1ST, 24x/SATA (135元，姑姑说她“想刻东西”…好吧…)
   总：2118元
   木有键鼠，木有机箱（机箱在运输过程中怕容易坏所以没买），木有显示器（暂时用旧的），OK。哦，还有运费40…

总结

久了不攒机真是out了啊out，殊不知现在流行显示核心嵌到CPU里面…而且也没想到硬盘由于工厂发大水涨价涨得厉害…哎
不过电脑这东西，平民级的用途的话，啥时候想用啥时候就买就行了，没有必要等，而且买了之后就没有什么好后悔的，因为这个行业的新产品出得太快了…当然也有人等着硬盘降价、等着显卡降价的，人家那不一样，人家那是发烧友，那是高玩，人家一个显卡就几千块的…能不等等么。

这是一道广为流传的题目: 编程判断两个链表是否相交;原题假设“不带环”，所以只要想通了之后很简单；但是，若要考虑带环的情况，那么要注意的点就很多了。 其实可以把无环和有环的情况全都包括在一个方法实现内解决。

分析

首先，无环的情况；无环是《编程之美》原书里的题目，很多人都反应说这个题相对书中其它题来讲太过于简单了。也确实，只要在纸上把“所有单向链表相交的情况”画出来很容易就能想通解法了（只要正确理解题意，那么“两个无环单向链表”画出来只可能是2条不相干的链表或一个”Y”字形） —— 所以，判断两个不带环的链表是否相交，只要将两个链表的头指针都移到链表尾，然后比较尾指针地址是否相等就可以了。 如果带环，个人总结，要明白以下几点：

1. 无环链表和有环链表是不可能相交的;
2. 两个有环链表若相交，其“整个环上”的所有node一定都重合;
3. 有环链表的相交，情况只有2种：相交于”环上”或相交于”不是环的部分”,即下图所示;两种情况都需要使用“两个指针的追逐”方法来判断两个链表的环部分是否相交;
4. 有关链表追逐的考虑: 相对速度、距离、时间要算好，否则很容易漏掉几种边界情况;