这是一道广为流传的题目: 编程判断两个链表是否相交;原题假设“不带环”，所以只要想通了之后很简单；但是，若要考虑带环的情况，那么要注意的点就很多了。 其实可以把无环和有环的情况全都包括在一个方法实现内解决。

分析

首先，无环的情况；无环是《编程之美》原书里的题目，很多人都反应说这个题相对书中其它题来讲太过于简单了。也确实，只要在纸上把“所有单向链表相交的情况”画出来很容易就能想通解法了（只要正确理解题意，那么“两个无环单向链表”画出来只可能是2条不相干的链表或一个”Y”字形） —— 所以，判断两个不带环的链表是否相交，只要将两个链表的头指针都移到链表尾，然后比较尾指针地址是否相等就可以了。 如果带环，个人总结，要明白以下几点：

1. 无环链表和有环链表是不可能相交的;
2. 两个有环链表若相交，其“整个环上”的所有node一定都重合;
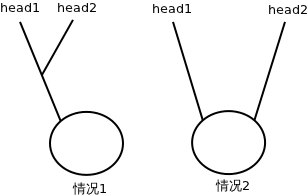
3. 有环链表的相交，情况只有2种：相交于”环上”或相交于”不是环的部分”,即下图所示;两种情况都需要使用“两个指针的追逐”方法来判断两个链表的环部分是否相交;
4. 有关链表追逐的考虑: 相对速度、距离、时间要算好，否则很容易漏掉几种边界情况;

代码

#include <stdio.h>

// define the node struct of links
typedef struct Node {
    struct Node* next;
} Node;

int is_intersected(Node* p1, Node* p2);

Node* has_circle(Node* head);

int main(int args, char** argv) {
    Node end1 = { NULL };
    Node end2 = { NULL };
    // 定义几种链表情况
    // two links not intersect with each other, no circle
    Node link_1_n =
            {
                    &(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&end1}}}}}}}}};
    Node link_2_n =
            {
                    &(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&end2}}}}}}}}};

    // two links intersect with each other, no circle
    Node common_n = { &(Node) {&(Node) {&end1}}};

    Node link_1_y = { &(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&common_n}}}}}};
    Node link_2_y = { &(Node) {&(Node) {&(Node) {&(Node) {&(Node) {&common_n}}}}}};

    // two links, has circle, not intersected.
    Node circle1 = { &(Node) {&(Node) {&(Node) {&(Node) {&circle1}}}}};
    Node link_c1_n = { &(Node) {&(Node) {&(Node) {&(Node) {&circle1}}}}};

    Node circle2 = { &(Node) {&(Node) {&(Node) {&(Node) {&circle2}}}}};
    Node link_c2_n = { &(Node) {&(Node) {&(Node) {&(Node) {&circle2}}}}};

    // two links, has circle, intersected at a non-circle position
    Node common_c = { &(Node) {&(Node) {&(Node) {&(Node) {&common_c}}}}};
    Node common_part = { &(Node) {&common_c}};

    Node link_c1_y = { &(Node) {&(Node) {&common_part}}};
    Node link_c2_y = { &(Node) {&(Node) {&common_part}}};
    // two links, has common circle, but different 'joint-points'.

    Node jp1 = { NULL };
    Node jp2 = { NULL };
    // 'weave' the joint-points into a circle:
    jp1.next = &(Node) {&(Node) {&jp2}};
    jp2.next = &(Node) {&jp1};

    Node link_c1_y2 = { &(Node) {&(Node) {&(Node) {&(Node) {&jp1}}}}};
    Node link_c2_y2 = { &(Node) {&(Node) {&(Node) {&(Node) {&jp2}}}}};

    if (is_intersected(&link_1_n, &link_2_n)) {
        printf("link_1_n and link_2_n Intersected!\n");
    }

    if (is_intersected(&link_1_y, &link_2_y)) {
        printf("link_1_y and link_2_y Intersected!\n");
    }

    if (is_intersected(&link_c1_n, &link_c2_n)) {
        printf("link_c1_n and link_c2_n Intersected!\n");
    }

    if (is_intersected(&link_c1_y, &link_c2_y)) {
        printf("link_c1_y and link_c2_y Intersected!\n");
    }

    if (is_intersected(&link_c1_y2, &link_c2_y2)) {
        printf("link_c1_y2 and link_c2_y2 Intersected!\n");
    }
    return 0;
}

int is_intersected(Node* p1, Node* p2) {
    Node* has_circle_1 = has_circle(p1);
    Node* has_circle_2 = has_circle(p2);

    if (has_circle_1) {
        if (has_circle_2) {
            Node* pp1 = has_circle_1;
            Node* pp2 = has_circle_2;
            if (pp1 == pp2 || pp1->next == pp2)
                return 1;
            while (pp1->next != has_circle_1) {
                pp1 = pp1->next;
                pp2 = pp2->next->next;
                if (pp1 == pp2)
                    return 1;
            }
            return 0;
        } else {
            return 0;
        }
    } else {
        if (has_circle_2) {
            return 0;
        } else {
            while (p1->next)
                p1 = p1->next;
            while (p2->next)
                p2 = p2->next;
            return p1 == p2;
        }
    }
    return 0;
}

Node* has_circle(Node* head) {
    Node* p1;
    Node* p2;
    p1 = p2 = head;
    if (p2->next != NULL) {
        p2 = p2->next;
    } else {
        return NULL;
    }
    while (p2->next != NULL && p2->next->next != NULL) {
        p1 = p1->next;
        p2 = p2->next->next;
        if (p1 == p2)
            return p1;
    }
    return NULL;
}

其中，has_circle方法是判断一个单向链表是否带环的，基本原理就是设置2个“速度”不同的链表，快的去追慢的，追上就是带环，直到较快指针遇到null还没追上就是没有环；假设环包含n个节点，指针p2的”速度”是2，p1的速度是1，相对速度就是1，从相同一点出发的话，p2追上p1至少要n步；若再假设该链表除了环的部分外还带有一个长度为k的“尾巴”，那么追上的步数最多是n+k;也就是线性时间复杂度内就能完成这个判断。

这提供了一种很好的判断是否”环状”的思路；以前我只写过“用一个栈来记录”的方式，弱爆了…(时间复杂度为O(n²))

在has_circle_1和has_circle_2都满足的时候，也就是说2个链表都带环的时候，要分别取2个环上的一点来玩“追逐游戏”来判断是否相交；在这段程序里是pp1和pp2;然后一个速度为2一个速度为1开始玩“追逐游戏”，当慢的那个走完环上所有节点时快的那个还没追上它的话，说明不相交(此时耗费时间n——即环节点数;因为快慢指针的相对速度为1，快指针理应在时间n以内追上慢链表，否则不相交)。

总结

单向链表的问题…着实不简单，可以相当复杂…对于这种关乎“形状”的问题，在纸上画一画会很有帮助。