Meta-Interpretation

Code, better explained.

LL(*)的概念与实现

| Comments

概念和起源

LL(*)是由Terrence Parr教授创造的，为使用LL分析的语法解析器做超前查看(look ahead)的一种算法。按照Parr教授的说法，这个算法从最初的想法至今的完善和调整已经历了15年。目前该算法的一个著名的实现在antlr3中。

特点，n言以蔽之…

  • 对于语法产生式分支的预测判断，走LL分析路子的解析器，其能力完全取决于能超前查看多少个token。传统地讲，LL(1), LL(2)直至LL(k)，就是在讲该解析器能够在语法分析过程中超前查看1, 2, k…个token。
  • 而LL(*)的意思就是，它在语法解析的过程中，超前查看的token个数不是固定的，是可伸缩的，不过这一点LL(k)分析也能做到(在k范围之内…)；
  • 但是，LL(*)还能越过一些重复出现的token，“到达”这些重复出现的token之后的token来做分析，这一点LL(k)是无法办到的(LL(k)无法意识到有token在循环出现，不管情况如何，它都将在尝试k个token之后放弃)；
  • 如果将超前查看的决策逻辑画成DFA的话，就是这样的一种形式：Look Ahead DFA
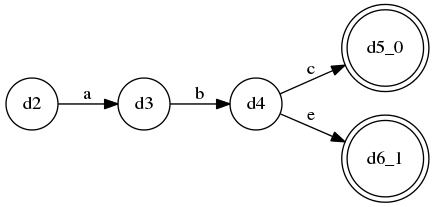
    • 这张图画的是这种语法规则的超前查看决策情况：A ::= a b c | a b e, 显然这是一个LL(3)语法；
    • 但是这样的语法: A ::= a b* c | a b* e是无法被LL(k)识别的，因为中间的b*代表“0个或多个b”(kleene闭包)，这并不是一个固定的重复次数，因此LL(k)无法识别，for any k…
    • 但是，LL(*)算法能够构造出这样的DFA来识别它：LL(*) Look Ahead DFA
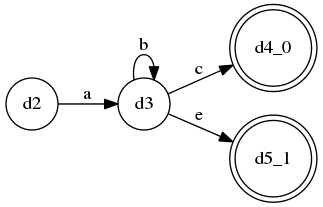
    • 也就是说，传统LL(k)的look ahead DFA是不带环的，而LL(*)算法能构造出带环的DFA来做判断，它能越过无穷多个存在于环上的token，从而“到达”环之后的token继续做判断。
  • 上面的A ::= a b* c | a b* e语法使用了“kleene闭包”表示法来表示“0个或多个”，这种表示法在正则表达式中很常见；事实上，基于LL(*)算法实现的语法解析器生成器(比如antlr3)对Kleene闭包表示法特别友好，可以鼓励使用，还能顺便解决一些LL分析法所不允许的“左递归”。
  • 大多数情况来讲，LL(*)的识别能力弱于LR(k)，但也有少数情况是LR(k)识别不了但LL(*)可以的，所以LL(*)与LR(k)之间并没有严格的强弱顺序。
  • LL(*)本身对语法的识别能力也是有限的，比如它无法区分”具有相同的递归规则前缀”的多个分支，这种情况是要尽量避免的，大多数能够较容易地改写;
  • 对于LL(*)不能正确分析的情况，还能引入”Semantic Predicate”(语义断言)来辅助判断, Semantic Predicate可以是任何逻辑，只要返回一个bool值就行；有了Semantic Predicate的辅助，LL(*)甚至能够parse一些上下文相关的语法，实际上它能parse C++

主要算法及其实现(python)

Parr教授在2011年发表的paper”LL(*): The Foundation of the ANTLR Parser Generator”中详细描述了这个算法，下面就是其主要过程，具体的代码实现(python)在工程llstar中

为了简单起见，约定大写字母用来命名non-terminal, 小写字母命名terminal或Semantic Predicate，$表示EOF，假设有如下语法规则：

S ::= A $  
A ::= a c*  
    | b c*
  • 针对此语法规则，构造Augmented Transition Network(ATN)，其实也就是一个NFA，NFA的边就是terminal或non-terminal或者Semantic predicate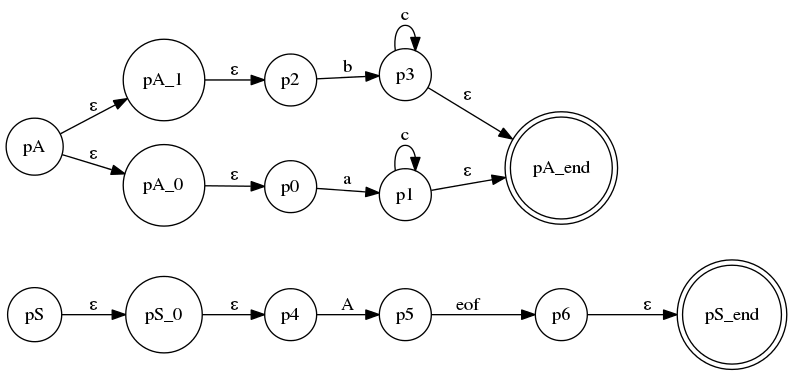：ATN network, 代码在llstar工程的atn_creation.py的rule.merge_to_atn方法中。
  • 接下来将要对这个ATN实施的算法其实就是经典的Subset Construction算法 —— 的改造版本：在“空边闭包运算(closure)”中加入了压栈、出栈功能，用于处理运算过程中closure函数经过non-terminal边时对其所对应的ATN的调用和返回。
    这个算法的具体描述是比较复杂，在Parr教授的paper中已有精确描述。不过真的要用代码实现起来，某些细节还需稍微修饰，才能正确地实现。
    最后的结果，其实就是使用更改后的版本的Subset Construction算法，将上述ATN(NFA)转化为一个个DFA，每条语法规则都对应一个DFA作为其look ahead DFA。
    例如上面的S规则最后的DFA为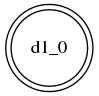：S DFA, well, 就一个终结态，没任何状态转换 —— 这是当然的，S规则只有一个alternative production…
    而A规则的DFA为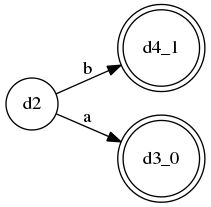：A DFA, 意思就是，如果第一个token为a，就选择第一个分支，若是b，就选择第二个分支，这是一个LL(1)的语法。
    简单来说就是这样，具体可以参考llstar的代码…这花了我不少时间调试出来的代码，还是直接看代码了解最直接:)

实验台及例子介绍

OK，主要的算法原理了解之后，展示了2个玩具例子，似乎还不能看出LL(*)的特点来。
下面我将逐步展示一些真正non-trivial的例子，以表明它真的不是过家家…

LL(3)(更正：或许这该是LL(4)可能我数错了)语法(对应llstar工程中的LL_3_many_alts.py):

S ::= A $
A ::= B a*
    | C a+
    | D a?
B ::= a b c C
    | a b c D
    | d
C ::= e f g D
    | e f g h
D ::= i j k l
    | i j k m

这个语法是固定的LL(3)，没有什么特别，不过分支比较多, 它的ATN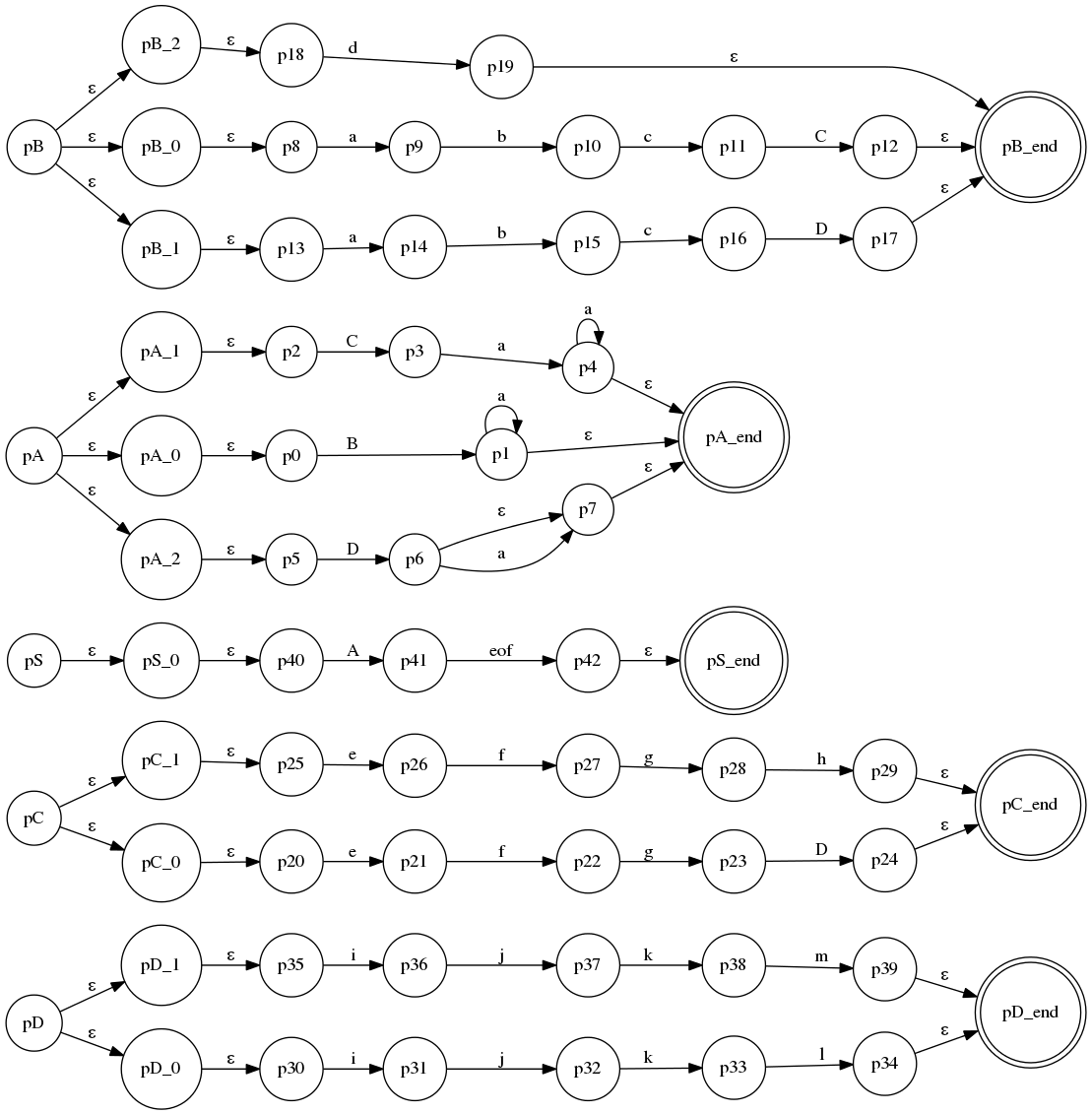：LL(3) ATN
规则A的DFA: 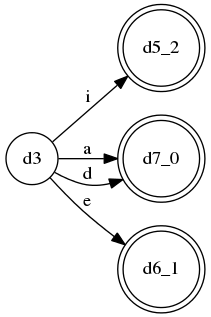LL(3) Rule A DFA
规则B的DFA: 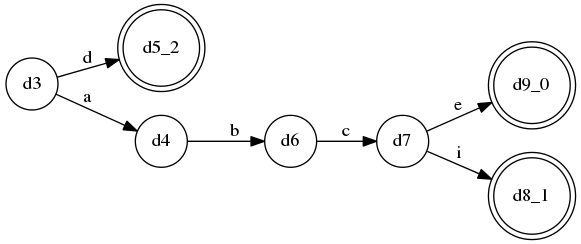LL(3) Rule B DFA
规则C的DFA: 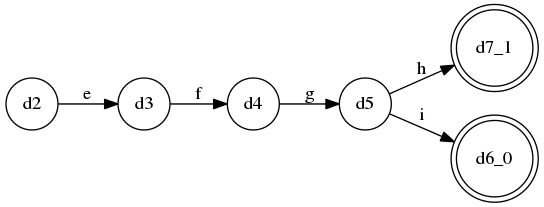LL(3) Rule C DFA
规则D的DFA: 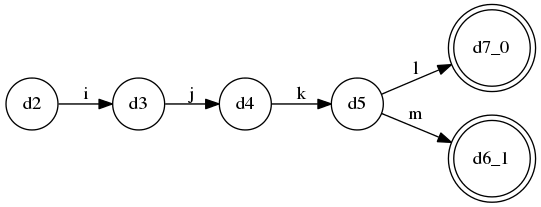LL(3) Rule D DFA

上面这个语法，LL(4)分析也能搞定，而真正体现出LL(*)特点的是下面这样的语法(对应llstar工程中over_kleene.py)：

S ::= A $
A ::= a* b
    | a+ c

其中，规则A的2条分支拥有共同的kleene闭包前缀，LL(k)是无法识别的，它的ATN: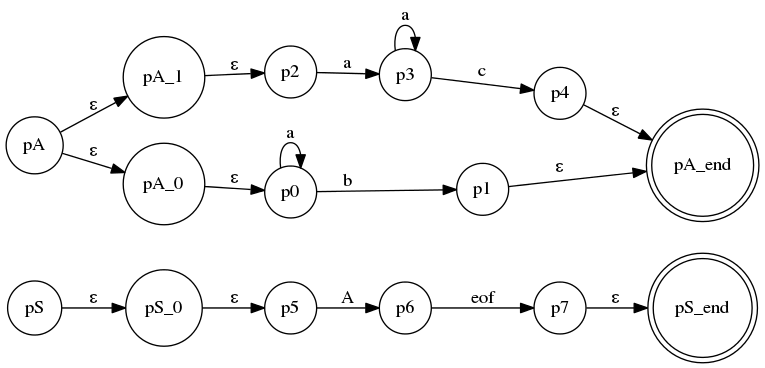Over Kleene ATN
而LL(*)能够为A生成这样的DFA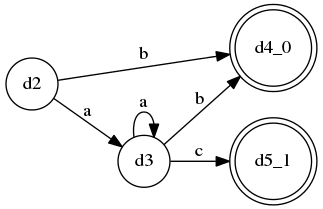：Over Kleene Rule A DFA
这个DFA能够越过terminala的任意重复，从而考虑到后面的terminalb和c来做判断
而下面这个更加”恶劣”的列子则更能说明LL(*)的这个特征(对应llstar工程中over_non_recurse_rule.py)：

S ::= A $
A ::= B* b
    | C+ c
B ::= a d
    | e
C ::= a d
    | e

这个例子中，B和C完全相同，并分别被包含在规则A的2条分支的kleene闭包中，
最终生成的A的DFA: 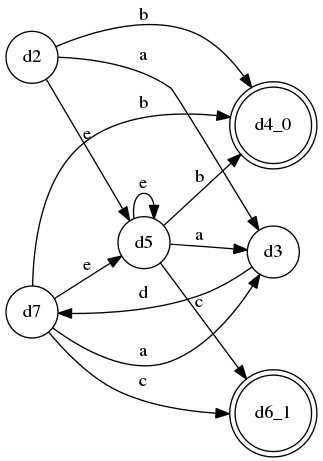Non-recursive Rule A DFA

上面提到过，LL(*)也有不能解决的情况，比如2条分支拥有”共同的、递归的规则作为前缀”，比如这样：

S ::= A eof
A ::= E a
    | E b
E ::= c E d
    | e

上面的A规则的两条分支拥有共同的前缀E，而E本身是一条递归规则，这样的规则是LL(*)无法分析的，在llstar工程中对应experiments/common_recurse_prefix_fail.py, 运行的时候会抛出错误提示。这种情况在antlr3中会将parsing策略退化为LL(1) + 回溯的形式。

Traceback (most recent call last):
  File "/home/pf-miles/myWorkspace/llstar/experiments/common_recurse_prefix_fail.py", line 31, in <module>
    d_a = create_dfa(ra.get_start_state(globals_holder.a_net))
  File "/home/pf-miles/myWorkspace/llstar/algos.py", line 136, in create_dfa
    d_state_new.add_all_confs(closure(d_state, conf))
  File "/home/pf-miles/myWorkspace/llstar/algos.py", line 99, in closure
    raise Exception("Likely non-LL regular, recursive alts: " + str(d_state.recursive_alts) + ", rule: " + str(globals_holder.a_net.get_rule_of_state(p)))
Exception: Likely non-LL regular, recursive alts: set([0, 1]), rule: E

还有一些特殊情况，比如规则完全就是冲突的，那么这个时候就是Semantic Predicate发挥作用的时候(对应llstar工程中conflicting_with_preds.py)：

S ::= A $
A ::= {pred1}? B
    | {pred2}? b
B ::= b
    | b

最终A的DFA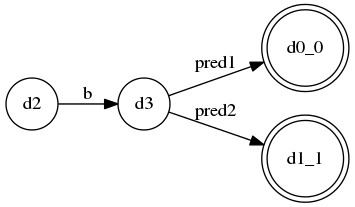：Conflict Resolved With Preds A DFA
实际开发中，写出这样的规则是坑到爷的…不过LL(*)还算能很好解决…其实这里就算没有Semantic Predicate, LL(*)也能按照convention，“选择较早定义的语法分支”来解决。

还有就是在分析的过程中会导致分析栈溢出(不是程序语言的callstack的overflow, 而是LL(*)的closure操作维护的一个规则调用栈溢出)的时候，LL(*)也会使用Semantic Predicate来辅助判断, 比如规则(对应llstar中overflow_with_preds.py):

S ::= A $
A ::= {pred1?} B a
    | {pred2?} b* c
    | {pred3?} b* c
B ::= b+ B

规则A的三条分支全部存在严重冲突(都拥有能识别无穷个’b’的前缀)并且其中一个是另一条递归规则B，这种形式会导致LL(*)的分析栈溢出，不过仍然没关系，这样的情况能在溢出发生时，调用pred1、pred2和pred3来解决(这三个pred就是Semantic Precicate，是能包含任何逻辑但最终返回bool值的表达式)
生成的规则A的DFA: 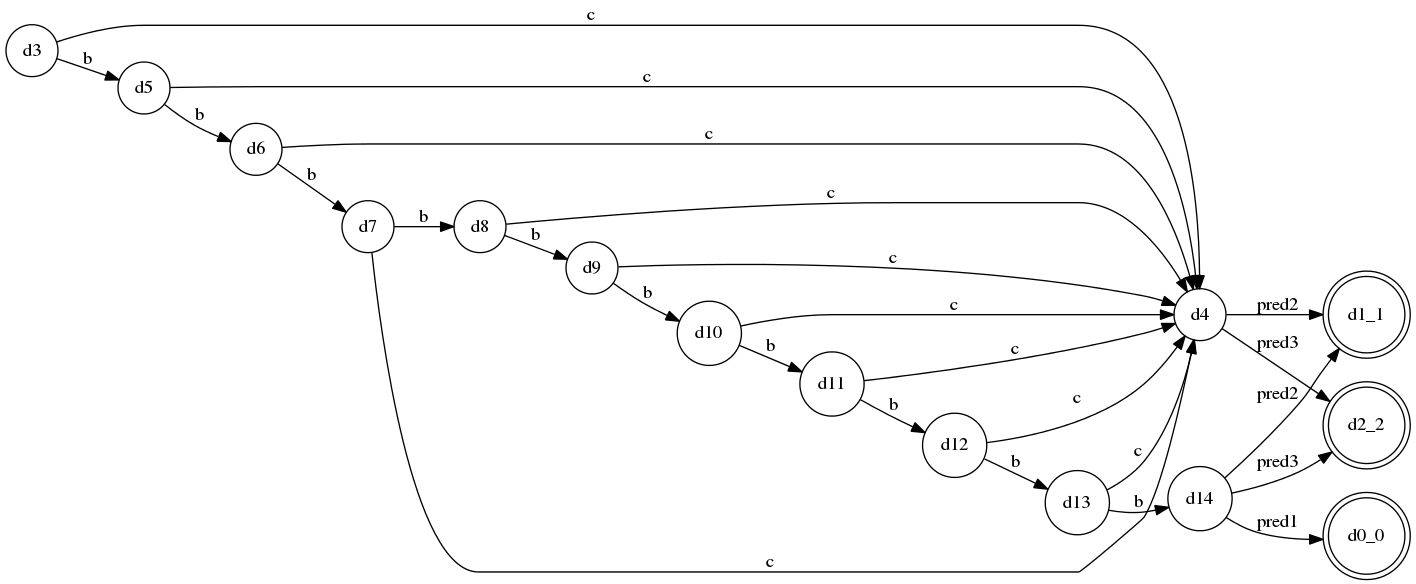Overflow A DFA
这里设定的最大分析递归层数为10，因此，DFA在接受了第10个’b’之后达到了溢出状态d14，这时调用了各个alternative附带的几个predicate来解决冲突…

(2012-09-03 注： 实际上上述规则是不正确的，B ::= b+ B是有问题的规则，因为b+会贪婪地match掉所有的连续的'b'，导致后面的B只可能抛错; 所以这个例子也只能用来演示分析栈溢出的情况，实际应用中是不可能写出这样的规则的)

总结

OK, 大概如是了；上述算法的实现、例子的代码均在llstar工程中能找到
llstar工程是我花了不少时间实现并调试好的一块LL(*)算法的“实验台”，可以在里面慢慢把玩各种变态的、五花八门的语法规则，以验证LL(*)的分析能力
在工程的experiments文件夹下已经有许多具有代表性的例子…都是python代码
另外，llstar工程是在eclipse + pydev环境下开发的，因此如果要在命令行里运行，可能要对例子里面的import路径稍作修改，当然，最好是直接在eclipse + pydev环境下运行它们了
在linux环境下，llstar的所有例子都能自动生成上文中看到的各种DFA/NFA图像，不过前提是环境中要装有graphviz

现在的所有语法解析器生成器中，似乎都是LR分析的天下，LL分析大多是手写解析器的首选…
不过在现有的使用LL分析方式的产品中，也就只有LL(*)和PEG(Packrat)parsing比较常见也比较实用了，能与LR分析一较高下。
而配上回溯策略的LL(*)是严格强于Packrat parsing的，这样看来大概走LL分析路子的自动化工具也只有LL(*)容易一枝独秀了(想必这也是antlr相对较为流行的原因)。

Comments